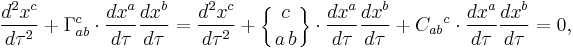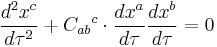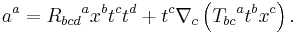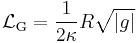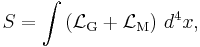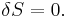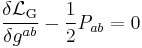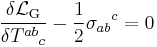Einstein–Cartan theory
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory or the Cartan–Sciama–Kibble theory is a classical theory of gravitation similar to general relativity but relaxing the assumption that the metric be torsion-free. Introducing torsion allows greater freedom to couple classical spin angular momentum to the metric. The theory was first proposed by Élie Cartan in 1922[1] and expounded in the following few years.[2] Dennis Sciama and Tom Kibble independently revisited the theory in the 1950s, and an important review was published in 1976.[3] Albert Einstein became affiliated with the theory in 1928 during his unsuccessful attempt to match torsion to the electromagnetic field tensor as part of a unified field theory. This line of thought led him to the related but different theory of teleparallelism.[4]
Einstein-Cartan theory has been historically overshadowed by its torsion-free counterpart and other alternatives like Brans–Dicke theory because torsion seemed to add little predictive benefit at the expense of the tractability of its equations. In particular, many effects of nonzero torsion are hypothesized to be non-propagating so that its direct observation is expected to be difficult.[5] Since Einstein-Cartan theory is purely classical, it also does not fully address the issue of quantum gravity. Interest in Einstein-Cartan theory has been renewed in recent years, however, as theorists try to incorporate torsion into novel quantum theories or as they explore its cosmological implications.[6] The theory is still considered viable and remains an active topic in the physics community.[7]
Contents |
Motivation
Spin-orbit coupling
Although general relativity can accommodate particles with spin, including spin-1/2, by using the tetrad formalism, it cannot couple the spin to orbital angular momentum. Spin-orbit coupling is a well documented phenomenon in quantum mechanics, so a theory of gravitation that hopes to be fit eventually into a quantum theory of gravity should be expected to incorporate spin directly into its field equations.
The reason that general relativity cannot describe spin-orbit coupling is rooted in Riemannian geometry, on which general relativity is based. In Riemannian geometry, the Ricci curvature tensor
must be symmetric in a and b (that is, Rab = Rba). Therefore the Einstein curvature tensor Gab defined as
must be symmetric. (gab is the metric tensor that defines lengths of vectors and inner products of pairs of vectors). In general relativity, the Einstein curvature tensor models local gravitational forces, and it is equal (up to a gravitational constant) to the momentum tensor
(We denote the stress-energy tensor by 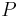 because the customary symbol
because the customary symbol 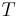 in general relativity is used in Einstein–Cartan theory to denote affine torsion. The momentum tensor is also called the stress-energy tensor, the energy-momentum tensor, and the energy-momentum-stress tensor. Special relativity shows that energy, momentum, momentum flux, and stress are different spacetime components of the same covariant object, known most compactly as the momentum tensor.)
in general relativity is used in Einstein–Cartan theory to denote affine torsion. The momentum tensor is also called the stress-energy tensor, the energy-momentum tensor, and the energy-momentum-stress tensor. Special relativity shows that energy, momentum, momentum flux, and stress are different spacetime components of the same covariant object, known most compactly as the momentum tensor.)
The symmetry of the Einstein curvature tensor forces the momentum tensor to be symmetric. However, when spin and orbital angular momentum are being exchanged, the momentum tensor is known to be nonsymmetric according to the general equation of conservation of angular momentum
- (divergence of spin current)
 (
(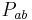 –
– 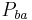 )
) 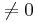 .
.
(See spin tensor for more details.)
Therefore general relativity cannot properly model spin-orbit coupling.
In 1922 Élie Cartan conjectured that general relativity should be extended by including affine torsion, which allows the Ricci tensor to be non-symmetric. Although spin-orbit coupling is a relatively minor phenomenon in gravitational physics, Einstein–Cartan theory is quite important because
- (1) it makes clear that an affine theory, not a metric theory, provides a better description of gravitation;
- (2) it explains the meaning of affine torsion, which appears naturally in some theories of quantum gravity; and
- (3) it interprets spin as affine torsion, which geometrically is a continuum approximation to a field of dislocations in the spacetime medium.
The extension of Riemannian geometry to include affine torsion is known as Riemann–Cartan geometry.
ω-consistency
General relativity is acknowledged to be ω-inconsistent in the sense that there is a limit of the theory that is not in the theory. Consider a fluid of rotating black holes. These black holes possess orbital angular momentum only and can be seated in a torsion-free spacetime. In the continuum limit, however, the angular momentum turns into spin angular momentum, and the metric becomes contorted. As the limit has torsion, it is not allowed in general relativity by assumption. Einstein-Cartan theory can thus be viewed as the minimal, ω-consistent extension of general relativity.
A mathematical proof has been published that general relativity plus a fluid of many tiny rotating black holes generate affine torsion that enters the field equations exactly as in the equations of Einstein–Cartan theory (Petti, 1986). If we introduce a classical spin fluid with spin-orbit coupling, torsion is necessary to describe the spin-orbit coupling. (Example of a classical spin fluid: Approximate a distribution of galaxies with correlated rotations as a classical fluid with spin. In this approximation, the rotational angular momentum of the galaxies becomes intrinsic angular momentum, that is, spin.) The mathematical proof starts with a standard Kerr-Newman rotating black hole solution of general relativity, and it computes the non-zero time-like translation that occurs when you parallel-translate an affine frame (keeping track of translation as well as rotation) around an equatorial loop near the black hole. The main conclusion (that general relativity plus spin-orbit coupling implies nonzero torsion and Einstein–Cartan theory) is derived from classical general relativity and classical differential geometry without recourse to quantum mechanical spin or spinor fields.
The proof consists of these four steps.
- Start with a Kerr-Newman rotating black hole. Compute the translational holonomy around an equatorial spacelike loop of constant radius.
- Construct an ensemble of very many very small rotating black holes with correlated rotations and take the continuum limit.
- In the continuum limit, the translational holonomy becomes affine torsion, the distribution of rotating black holes generates spin density, and the torsion and spin density are related exactly as in Einstein-Cartan theory.
- For completeness, compute the translational holonomy for loops in other hyperplanes, to prove that the other loops generate no affine torsion in the continuum limit.
Adamowicz showed that general relativity plus a linearized classical model of matter with spin yields the same linearized equations for the time-time and space-space components of the metric as linearized Einstein–Cartan theory (Adamowicz 1975). Adamowicz does not treat the time-space components of the metric, the spin-torsion field equation, spin-orbit coupling and the non-symmetric momentum tensor, the geometry of torsion, or quantum mechanical spin. Also, Adamowicz does not show that Einstein–Cartan theory follows from general relativity plus spin. He says, “It is possible a priori to solve this problem [of dust with intrinsic angular momentum] exactly in the formalism of general relativity but in the general situation we have no practical approach because of mathematical difficulties.” Adamowicz’s conclusion is at best incomplete: it is not possible to solve the full problem exactly in general relativity, including spin-orbit coupling, without adopting the larger framework of Einstein–Cartan theory.
Mathematical background
The two most important concepts in Einstein-Cartan theory that may be new to the general relativist are the understanding of the torsion tensor and how it relates to the spin tensor. Since torsion is a more mathematical than phenomenological concept, we will discuss it first. The reader should be familiar with the mathematical foundation of general relativity at the level of Wald, whose notation and axiomatic approach have been borrowed. An appropriate accompanying text in the same notation is online[1] and may be useful to the beginner. The equations below use abstract index notation with implied summation over repeated indices unless otherwise noted. Brackets denote the antisymmetric part of a tensor.
A covariant derivative is an operator satisfying four defining properties.
- Linearity:
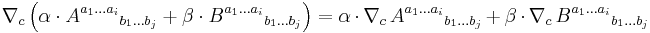
- Product rule:
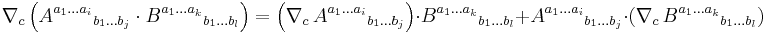
- Commutativity with tensor contraction (summation emphasized):
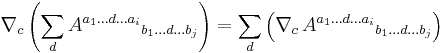
- A tangent vector is a directional derivative of a scalar field:
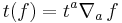
Given a symmetric (0,2) tensor 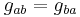 called the metric tensor and an antisymmetric (1,2) tensor
called the metric tensor and an antisymmetric (1,2) tensor 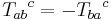 known as the torsion tensor, there exists a unique covariant derivative denoted by a semicolon with two extra properties.
known as the torsion tensor, there exists a unique covariant derivative denoted by a semicolon with two extra properties.
- Compatibility of the metric:
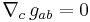
- Commutator of the covariant derivative:
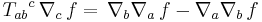
In the case 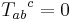 (torsion-free), this theorem is known as the fundamental theorem of Riemannian geometry. It is this torsion-free assumption that Einstein-Cartan theory relaxes. The uniqueness of the covariant derivative nevertheless remains assured for nonzero torsion. The torsion tensor may also be interpreted as an antisymmetric part of the Christoffel symbols:
(torsion-free), this theorem is known as the fundamental theorem of Riemannian geometry. It is this torsion-free assumption that Einstein-Cartan theory relaxes. The uniqueness of the covariant derivative nevertheless remains assured for nonzero torsion. The torsion tensor may also be interpreted as an antisymmetric part of the Christoffel symbols:
but such a relation is not manifestly covariant. If we define the general relativistic connection coefficient as
where we have used comma derivative notation, then we may define an auxiliary (1,2) tensor 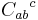 called the contortion tensor defined by
called the contortion tensor defined by
where we note again that the last relation is not manifestly covariant. While the loss of symmetry is more general, it complicates many of the equations relevant to understanding curvature. For example, the Riemann curvature tensor now behaves nontrivially under certain permutations of its indices:
The Bianchi identity must also be adjusted:
Likewise, the Ricci tensor is no longer symmetric but instead has the property
Geometric intuition
In order to understand why torsion should be related to spin, we can consider how the presence of torsion may affect observers living in contorted spacetime. The first equation to consider is the geodesic equation, which is unchanged. We may alternatively rewrite the geodesic equation in terms of the contortion tensor defined above:
where  is the proper time. This shows that the connection can be split into pure metric and pure torsion contributions. In the limit of Minkowski spacetime
is the proper time. This shows that the connection can be split into pure metric and pure torsion contributions. In the limit of Minkowski spacetime 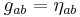 and a completely antisymmetric torsion tensor
and a completely antisymmetric torsion tensor ![T_{abc}=T_{[abc]}](/2012-wikipedia_en_all_nopic_01_2012/I/55c5d8d91beb0bff2735fa8d15b94921.png) , a vector parallelly transported along a geodesic (i.e. straight line for Minkowski spacetime) described by the reduced equation
, a vector parallelly transported along a geodesic (i.e. straight line for Minkowski spacetime) described by the reduced equation
rotates about the translation axis.
The geodesic deviation equation is modified in the presence of torsion. Let 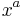 be a deviation vector between two infinitesimally neighboring geodesics, and let
be a deviation vector between two infinitesimally neighboring geodesics, and let 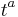 be a tangent to the geodesics along which
be a tangent to the geodesics along which 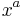 is transported. The modified geodesic deviation equation that expresses the acceleration between neighboring geodesics is
is transported. The modified geodesic deviation equation that expresses the acceleration between neighboring geodesics is
Whereas the Riemann curvature applies a tidal acceleration, the torsion causes the geodesics to twist around each other. The infinitesimal picture must be emphasized. Imagine a rod made up of a lattice of particles. The relative positions of the particles are fixed to be at the spacing of the lattice, but the particles are otherwise non-interacting. As the rod moves along, the rod as a whole does not rotate but rather each of the infinitesimally small particles making up the rod will want to spin about its own axes.
Field equations
The fundamental equations of any field theory are declared as brute facts, for example D'Alembert's principle in Newtonian mechanics. It is epistemically useful, however, to consider the more restricted class of field equations that can be derived by a variational principle applied to an action because this eases the implementation of Noether's theorem or one of its analogs. For example, the Einstein field equations of general relativity can be derived, among other ways, by postulating the Einstein-Hilbert action to be the true action of spacetime and then varying that action with respect to the metric tensor. The field equations of Einstein-Cartan theory come from the exact same approach. Let 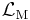 represent the Lagrangian density of matter and
represent the Lagrangian density of matter and 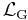 represent the Lagrangian density of gravitation. We use the convention that Lagrangian densities are tensor densities. First, the Einstein-Hilbert action is postulated, i.e. the Lagrangian density of gravitation is assumed to be the Ricci scalar (up to an overall constant),
represent the Lagrangian density of gravitation. We use the convention that Lagrangian densities are tensor densities. First, the Einstein-Hilbert action is postulated, i.e. the Lagrangian density of gravitation is assumed to be the Ricci scalar (up to an overall constant),
where  is the determinant of the metric, and
is the determinant of the metric, and  is a physical constant
is a physical constant 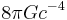 involving the gravitational constant and the speed of light. By Hamilton's principle, the total variation of
involving the gravitational constant and the speed of light. By Hamilton's principle, the total variation of  should vanish:
should vanish:
Variation with respect to the metric 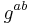 yields equations reminiscent of general relativity:
yields equations reminiscent of general relativity:
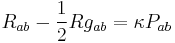 |
where 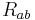 is the Ricci tensor and
is the Ricci tensor and 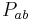 is the canonical energy-momentum tensor. The reader must be cautioned that, despite similarity of form, this is not the same as the Einstein field equation because the Ricci tensor is no longer symmetric but instead contains information about the nonzero torsion tensor as well. The right hand side of the equation cannot be symmetric either, so
is the canonical energy-momentum tensor. The reader must be cautioned that, despite similarity of form, this is not the same as the Einstein field equation because the Ricci tensor is no longer symmetric but instead contains information about the nonzero torsion tensor as well. The right hand side of the equation cannot be symmetric either, so 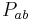 must also contain information about the nonzero spin tensor. This canonical energy-momentum tensor is related to the more familiar symmetric energy-momentum tensor by the Belinfante–Rosenfeld procedure.[8]
must also contain information about the nonzero spin tensor. This canonical energy-momentum tensor is related to the more familiar symmetric energy-momentum tensor by the Belinfante–Rosenfeld procedure.[8]
We may also consider the variation of  with respect to the torsion tensor
with respect to the torsion tensor 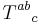 . This yields a new equations
. This yields a new equations
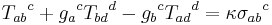 |
where 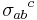 is the spin tensor. Note that in the first field equation, the trace of the Ricci tensor has been modified. Compare to the second field equation, where the trace of the torsion tensor has been altered. The steps between the variation of the action to the final field equations are given in the appendix of the Hehl et al. review.
is the spin tensor. Note that in the first field equation, the trace of the Ricci tensor has been modified. Compare to the second field equation, where the trace of the torsion tensor has been altered. The steps between the variation of the action to the final field equations are given in the appendix of the Hehl et al. review.
Basis for loop quantum gravity
In 1986, physicist Abhay Ashtekar completed the project which Amitabha Sen began. He clearly identified the fundamental conjugate variables of spinorial gravity: The configuration variable is as a spinoral connection - a rule for parallel transport (technically, a connection) and the conjugate momentum variable is a coordinate frame (called a vierbein) at each point. So these variables became what we know as Ashtekar variables, a particular flavor of Einstein–Cartan theory with a complex connection. General relativity theory expressed in this way, made it possible to pursue quantization of it using well-known techniques from quantum gauge field theory.
Other basic physical theories that employ affine torsion
For completeness, below are references to some speculative physical theories that employ torsion in ways that are different from Einstein–Cartan theory.
There are proposals to describe what is called propagating torsion.[9][10][11][12][13][14][15][16] This is done by expressing the torsion as a gradient of some other field which propagates. However, since the torsion couples directly to spin, the propagating field couples to the gradient of the spin current density, so that the interaction is again completely local (it leads to a four-Fermi interaction), and the effect of torsion cannot propagate away from matter after all. Moreover, the photon has spin 1, but the torsion must be forbidden to couple to it, since the photon is so far the lowest-mass particle in the universe. But if torsion coupled to the spin-1/2 electrons and protons, this will make the photons massive by vacuum polarization.
To avoid these problems, the only way out so far is to assume for the gauge field description of the Einstein-Cartan Theory the Einstein action in the teleparallel form, where torsion is just an equivalent alternative to curvature.[17]
Moreover, it can be shown that there exists an infinity of equivalent descriptions where any amount of torsion can be moved into Cartan curvature. All these theories are connected by a new type of multivalued gauge transformations.[18]
See also
References
- ^ Élie Cartan. "Sur une généralisation de la notion de courbure de Riemann et les espaces à torsion." C. R. Acad. Sci. (Paris), 174:593–595, 1922.
- ^ Élie Cartan. "Sur les variétés à connexion affine et la théorie de la relativité généralisée." Part I: Ann. Éc. Norm. 40: 325–412 and ibid. 41: 1–25; Part II: ibid. 42: 17–88
- ^ Friedrich W. Hehl, Paul von der Heyde, G. David Kerlick, and James M. Nester. "General relativity with spin and torsion: Foundations and prospects." Rev. Mod. Phys. 48, 393–416 (1976) http://link.aps.org/doi/10.1103/RevModPhys.48.393
- ^ Hubert F. M. Goenner. "On the History of Unified Field Theories." Living Rev. Relativity, 7, (2004), 2.
- ^ Sean Carroll and George Field. "Consequences of Propagating Torsion in Connection-Dynamic Theories of Gravity." Phys. Rev. D50 (1994) 3867-3873.
- ^ Nikodem Poplawski. "Cosmology with torsion: An alternative to cosmic inflation." Phys. Lett. B694:181-185, 2010; Erratum-ibid. B701:672, 2011.
- ^ Friedrich Hehl. "Note on the torsion tensor." Letter to Physics Today. March 2007, page 16.
- ^ R. Aldrovandi, J. G. Pereira. "Gravitation: in search of the missing torsion." Ann. Fond. Louis de Broglie 32 (2007) 229.
- ^ Propagating torsion 1: Consequences of Propagating Torsion in Connection-Dynamic Theories of Gravity
- ^ P. t. 2: Propagating torsion and gravitation
- ^ P. t. 3: Gravity theories with propagating torsion
- ^ P. t. 4: Scalar-tensor theory and propagating torsion theory
- ^ P. t. 5: Macroscopical consequences of a propagating torsion potential
- ^ P. t. 6: Propagating torsion as a massive vector field
- ^ P. t. 7: A Discussion on Massive Gravitons and Propagating Torsion in Arbitrary Dimensions
- ^ P. t. 8: Propagating Torsion without Spin
- ^ De Andrade V.C., Arcos H.I., Pereira J.G., Class. Quant. Grav. 21, 5193 (2004) ("Torsion as Alternative to Curvature in the Description of Gravitation")
- ^ Kleinert, H., "New Gauge Symmetry in Gravity and the Evanescent Role of Torsion"
Further reading
- Breton, R. P., et al. (2008). Science 321(5885), 104-107.
- Adamowicz, W. (1975). Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 23 (1975), no. 11, 1203-1205.
- Cartan, E. (1922). Comptes Rendus 174, 437-439, 593-595, 734-737, 857-860, 1104-1107.
- Gronwald, F. and Hehl, F. W. (1996). On the Gauge Aspects of Gravity gr-qc/9602013
- Hehl, F. W. and B. K. Datta (1971). J. Math. Phys., 12, 1334.
- Hehl, F. W. (1973). Gen. Rel. Grav., 4, 333.
- Hehl, F. W. (1974). Gen. Rel. Grav., 5, 491.
- Hehl, F. W., von der Heyde, P., Kerlick, G. D., and Nester, J. M. (1976). Rev. Mod. Phys. 48, 393.
- Kerlick, G. D. (1975). thesis, Department of Physics, Princeton U.
- Kibble, T. W. B. (1961). J. Math. Phys., 2, 212.
- Kleinert, H. (1987). In "Gauge Fields in Condensed Matter" (World Scientific). See especially “Part IV: Differential Geometry of Defects and Gravity with Torsion.”
- Kleinert, H. (2000). Gen. Rel. Grav. 32, 769.
- Kleinert, H. (2008), Multivalued Fields in Condensed Matter, Electrodynamics, and Gravitation. (World Scientific) (online)
- Petti, R. J. (1976). "Some Aspects of the Geometry of First Quantized Theories" Gen. Rel. Grav. 7, 869-883.
- Petti, R. J. (1977). "Some Aspects of the Geometry of First Quantized Theories II" Gen. Rel. Grav. 8, 887-903.
- Petti, R. J. (1986). "On the Local Geometry of Rotating Matter" Gen. Rel. Grav. 18, 441-460. Erratum: The definition of Palatini torsion S (called "modified torsion" in the 1986 paper) contains a factor of two that, while arbitrary, causes confusion, and is omitted in this article. When this change is made, the discussion in the middle of section 4.3 of an anomalous factor of 2 should be omitted.
- Petti, R. J. (2001). "Affine Defects and Gravitation" Gen. Rel. Grav. 33, 209-217. Erratum: The right-hand side of equation (10) is missing an additional term based on the antisymmetric part of the contortion tensor K.
- Petti, R. J. (2006). Translational spacetime symmetries in gravitational theories Class. Quantum Grav. 23, 737-751.
- Poplawski, N. J. (2009). Spacetime and fields, arXiv:0911.0334
- Poplawski, N. J. (2010). Cosmology with torsion - an alternative to cosmic inflation, arXiv:1007.0587
- de Sabbata, V. and Sivaram, C., "Spin and Torsion in Gravitation", World Scientific 1994.
- Saa, A. (1993). Einstein–Cartan theory of gravity revisited, gr-qc/9309027
- Sciama, D. W. (1964). Rev. Mod. Phys., 36, 463.
|
|
|||||
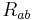
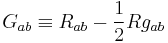
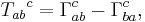
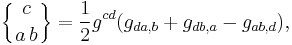
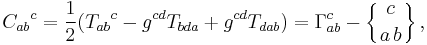
![{R_{[abc]}}^d={T_{[ab}}^e {T_{c]e}}^d - \nabla_{[a} {T_{bc]}}^d](/2012-wikipedia_en_all_nopic_01_2012/I/c2ed1aa97d9654b0fb35df9ac580fe13.png)
![R_{cdab}=R_{abcd}%2B\frac{3}{2} \left( \nabla_{[b} T_{cd]a} - \nabla_{[a}T_{cd]b} - \nabla_{[d}T_{ab]c} %2B \nabla_{[c}T_{ab]d} %2B T_{e[b|a|}{T_{cd]}}^e - T_{e[a|b|}{T_{cd]}}^e - T_{e[d|c|}{T_{ab]}}^e %2B T_{e[c|d|}{T_{ab]}}^e \right) .](/2012-wikipedia_en_all_nopic_01_2012/I/b5b779bc92d558d13078a58b743c2511.png)
![{\nabla_{[a} {R_{bc]d}}^e={T_{[ab}}^f{R_{c]fd}}^e} .](/2012-wikipedia_en_all_nopic_01_2012/I/9d7ab89746e1603fa80cc7e20715af6a.png)
![R_{ba}=R_{ab}%2B3 \nabla_{[a} {T_{cb]}}^c - {T_{cd}}^c{T_{ab}}^d .](/2012-wikipedia_en_all_nopic_01_2012/I/b76beb540201b45bc7e7d55afd692b75.png)